جمعه ۱۴ اردیبهشت ۱۴۰۳ / Friday 3rd May 2024

 

 

خَیاّم که خیمه‌های حکمت می‌دوخت

 
 
«خیام که خیمه‌های حکمت می‌دوخت»، بیتی از یک رباعی منسوب به خیام است که پاییز ۱۳۰۷ (حدود یک قرن پیش) اشرف‌السادات حسینی (ایران‌الدوله هلن)، در آغاز یک صفحه قدیمی خوانده‌است. خوانش وی تحریرهای قمر و ته صدای ملوک ضرابی را بیاد می‌آورَد. نورعلی خان برومند، و ناصرعلی‌خان حجازی با زخمه‌های تا‌ر، ایران‌الدوله را همراهی می‌کردند.
خیام که خیمه‌هایِ حکمت می‌دوخت - در بوته ی غم فتاد و ناگاه بسوخت
مقراضِ اجل طنابِ عمرش ببرید - دلال فلک به رایگانش بفروخت
سلام بر دوستان عزیز و اهل تمیز؛ دانشوران شریفی که بقول فردوسی «تارو پود»شان، داد و خرد است.
خانمها و آقایان محترم؛ من در سالهای گذشته از شهسوران میدان علم گفته و نوشته‌ام که برخی از آنها منتشر شده‌است. خردمندانی چون ابوعلی سینا؛ ابوحامد محمد غزالی، محمد بن زکریای رازی، غیاث الدین جمشید کاشانی، ابن هیثم، محمد بن موسی خوارزمی، ابوریحان بیرونی، خواجه نصیر طوسی، ابوالوفا بوزجانی، ابویوسف الکِندی، گالیله، یوهانس کپلر، نیوتن، آلبرت آینشتاین، استیون هاوکینگ، ادوارد سِیگِن، جان رالز، لئون فوکو (فوکالت)، توماس پین، برتراند راسل، دکارت، رابرت بویل، بیکن، گیلبرت لوییس و ارنست بلوخ، همچنین دکتر محسن هشترودی، دکتر غلامحسین مصاحب، دکتر علی جوان، پرویز شهریاری و مریم میرزاخانی...
...
اکنون به خیام؛ غیاث الدین ابوالفتح عمربن ابراهیم نیشابوری (۴۲۷ - ۵۱۰)، مبتکر هندسه تحلیلی و ریاضی‌دانِ برجسته در تاریخ علم می‌پردازم. رند فرزانه‌ای که با کوزه‌گر دهر، که جام لطیف می‌سازد و بر زمین می‌زندَش، چون و چرا می‌کرد و توهّم اراده آزاد را به چالش می‌گرفت.
به او خَیاّم می‌گفتند چون شغل پدرش خیمه‌دوزی بوده‌است. به این موضوع در جامع التواریخ رشیدالدین‌ فضل‌اللّه، تذکره الشعراء دولتشاه و «روضه الصفا»ی میرخواند و... اشاره شده‌است. خانم‌ها و آقایان محترم به لحاظ تاریخ علم، تاریخ فکر و تاریخ ادبیات، شناخت خَیاّم که خیمه‌های حکمت می‌دوخت، ضروری است. 
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
گرچه در یک رباعی منسوب به خَیاّم «سردفتر عالم معانی عشق است» و در سروده‌های او آمده «چون جود ازل بود مرا انشا کرد، بر من ز نخست درس عشق املا کرد»، هرچند به ماه و ستاره و خورشید مهر می‌ورزید، اما کمتر از عشق حرف می‌زند. او البته با خودش وحدت داشت و تصریح می‌کرد من بی میِ ناب زیستن نتوانم... با عشق زنده بود.
گفته شده «او جهان افلاطونی را واژگون کرد و دز نظرش بالا و پست وجود نداشت. حال آنکه نزد خیلی‌ها همان ساختمان صعودی - نزولی  و دردهای عاشقانه و نمادهای عشق عرفانی را بازمی‌یابیم.»
... 
در سروده‌های خیام؛ آن شاعر «لحظه‌هایِ برق آسای حضور»، ایمان و شک، اطاعت و عصیان و لحظه و ابدیت در مواجهه با یکدیگر قرار می‌‌گیرند و او دنیا را به سان تصاویری پی‌‌درپی می‌‌بیند که گِرد فانوس خیال، چندی پدیدار می‌‌شوند و سپس در «صندوق عام» ناپدید می‌شوند». خَیاّم در گرد و‌غبار پیش‌فرض‌ها و پیش‌گرایشِ ذهنی‌ بسیاری از ما گم شده و هر کسی از ظن خویش او را به‌اصطلاح «داوری» می‌کند. کسانیکه به هیستری ضدمذهبی افتاده‌اند، از او نردبان می‌سازند و شریعت‌مداران مرتجع به او رو تُرش می‌کنند. در گذشته نیز چنین بوده‌است. جمال‌الدین قِفْطی(۵۶۸- ۶۴۶هـ)معتقد بود که باطن شعرهای خیام، همچون مار، شریعت را نیش می‌زند... 
خیام با تهور اندیشه؛ فلسفه و کلام را عنان بر عنان، رد و روانه کرده‌است اما همه برداشت امثال جمال‌الدین قِفْطی را نداشتند. خیلی‌ها آزادگی خیام را می‌ستودند. گفته‌اند حکیم ابوالحسن رفیعی قزوینی (از آموزگاران سید جلال‌الدین آشتیانی) گفته بود: «خیام آزادترین، آزاده‌ترین و والاقدرترین کس در تمام طول تاریخ تفکر اسلامی است.»
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
نخستین منبعی که خَیاّم را معرفی کرده‌، چهار مقالهٔ نظامی عروضی است. وی به ملاقات خودش با خَیاّم در شهر بلخ اشاره نموده. ابوالحسن علی بیهقی، نیز از او یاد کرده‌است. این هر دو، هم‌دوره خَیاّم بوده و او را از نزدیک دیده‌اند. دیگر متون کهنی که کم و بیش مطالبی دربارهٔ خَیاّم و آثارش در آن‌ها یافت می‌شود عبارتند از:
  • میزان الحکمه از عبدالرحمان خازنی
  • خریدة القصر از عمادالدین کاتب اصفهانی
  • نزهة الروح از شهرزوری
  • مرصادالعباد از نجم‌الدین رازی
  • الکامل فی التاریخ از ابن اثیر
  • شذرات الذهب از ابن العماد حنبلی
  • آثار البلاد و اخبار العباد از زكريا قزوینی
  • همچنین، نحو القلوب قشیری و رسالهٔ الزاجر للصغار زمخشری، کهن‌ترین بُن‌مایه‌ها دربارهٔ خیام و زندگی او را در بردارد.
خَیاّم از این گزاره که «بر لوح نشان بودنی‌ها بوده‌است...» نتیجه خرافی نمی‌گیرد. زبان تند و تیزش در رباعیات، تازیانه‌ای بر زاهدانِ دروغین و ریاکار است و چون و چراها و شک‌اش بمراتب از یقین‌های کور مدعیان معرفت، به حقیقت نزدیک‌تر، و سرگردانی او از آرامش سیاه غنودگان حریم وصل، بسامان‌تر است. خَیاّم برای من ابوالعلا مُعِرّی (نویسنده رسالهُ الغُفران) را بیاد می‌آورد. شوریده و دردمندی که در حکومت متعصب و مستبد وقت فریاد می‌زد: مردم روزگار ما دو گونه‌اند: یا عقل دارند و دین ندارند، یا دین دارند و عقل ندارند!
این مباحث تا بدین‌جا گفتنی‌ست - هرچه آید زین سپس بنهفتنی‌ست
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ 
جهان خَیاّم بیرون از صورت‌ها و الگوهای ازلی، بیرون از حیطه‌ی ادیان و عروج و رستاخیز و معاد است. گرچه پایگاه علمی این حکیم فرهیخته، برتر از جایگاه ادبی اوست ولی آوازه‌اش بیشتر رباعیات اوست که امثال ایران‌الدوله، بنان و دلکش، شجریان، ام کلثوم، و محمد عبدالوهاب و...آنها را به آواز خوانده‌اند.
...
سخن خَیاّم (در رباعیاتش) بیش از آنکه لطیف باشد محکم است. البته هرچه از زمانه خَیاّم دورتر می‌شویم هم تعداد رباعیات منسوب به او بیشتر می‌شود، هم متن رباعیات مطابق ذوق و سلیقه‌ی مردم هر زمانه دستخوش تغییرات زیادی می‌شود.
...
انتخاب قالب رباعی برای بیان اندیشه از طرف خَیاّم قابل تامل است. رباعی در چهارچوب بنیان خود بی‌شباهت به صورت قضیه‌ای منطقی نیست چنانکه گویی کیفیت استنتاج حکمی را از اخکام دیگر عنوان می‌کند.
 
همانطور که می‌دانیم رباعیات خَیاّم به بیشترِ زبان‌های زنده دنیا برگردانده شده‌است. آوازهٔ وی در غرب به‌طور مشخص بیشتر مدیون ترجمهٔ (یا بهتر بگویم برداشت‌های) ادوارد فیتزجرالد از رباعیات او به زبان انگلیسی است.  رباعی (قالب دلخواه شعری خَیاّم) محصول یک آن قرارگرفتن شور و شعور گوینده در پرتو اشراق شعر و صید کردن آن لحظه‌ی ناب تکرارناپذیر است. بقول  شفیعی کدکنی «خَیاّم در رباعیاتش صدای حیرت انسانی است و در زمان حیاتش تکرار مرگ و زندگی در شکل‌گیری کارگاه کوزه‌گری در نیشابور تمثیلی آشنا بوده‌است.» 
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ 
من به حیرت خَیاّم و اینکه حتی کوزه‌گر دهر را که خَلَقَ الْإِنسَانَ مِن صَلْصَالٍ كَالْفَخَّارِ برتر از سؤال نمی‌داند، احترام می‌گذارم اما تمرکز من در این بحث، نه نگاه و دیدگاه فلسفی خَیاّم و رباعیات او، بلکه خَیاّم ریاضی‌دان و مبتکر هندسه تحلیلی و گاه‌شماری ایران است.
...
تاریخ گاه‌شماری ایرانی به بیش از چهارهزار سال پیش گاه‌شماری بابلی بازمی‌‌گردد. البته نیاکان ما نظام خورشیدی را برای گاه‌شماری‌ها بکار می‌بردند. بعد از شکل‌گیری حکومت هخامنشیان، گاه‌شماری در ایران تغییراتی کرد و گاه‌شماری زرتشتی  رسمیت یافت. با هجوم اعراب به ایران زمین، برای قرن‌ها گاه‌شماری قمری در کنار گاه‌شماری خورشیدی کاربرد داشت. با توجه به نیاز اجتماعی و اقتصادی جامعه و همچنین پیشرفت علوم در دوره اسلامی، دانشمندان ایرانی دست به مطالعه و اصلاح گاه‌شماری زدند.
به پیشنهاد نظام‌الملک و جلال‌الدوله ملکشاه سلجوقی، خَیاّم در اصفهان به رصد ستارگان مشغول شد و توانست طول سال را با دقت بسیاری به دست آورد. ۳۶۵.۲۴۲۲ روز که با آنچه اکنون می‌دانیم ۳۶۵.۲۴۲۱۸۹ تفاوت زیادی ندارد.
خَیاّم با اصلاح گاه‌شماری یزدگردی و ارائه گاه‌شمار جلالی، که به نام جلال الدوله ملکشاه سلجوقی نامگذاری شده، با دقیق‌ترین نظام گاه‌شماری خورشیدی، گام بزرگی برداشت.
...
نوروز مهم‌ترین ویژگی گاه‌شمار مزبور است. بقول زنده یاد محمد حیدری ملایری ایرانیان می‌توانند بر خود ببالند که دقیق‌ترین گاه‌شمار سنتی جهان را دارند. کاری که خَیاّم صورت داد چسباندن نقطه آغاز بهار به آغاز ماه فروردین بود. هیچ کس تا آنزمان نتوانسته بود چنین کار مهمی انجام دهد. توجه داشته باشیم که گاه‌شمار ایرانی، خورشیدی است و بر حرکت ظاهری سالانه خورشید نهاده شده‌است. سال خورشیدی مدت زمان میان دو گذر پیاپی خورشید از یک نقطه مُعیّن آسمان است. بهتر بگویم سال خورشیدی، فاصله زمانی دو عبور متوالی خورشید از نقطه اعتدال بهاری است.
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ  
خورشید در طول سال نسبت به ستارگان ثایت از غرب به شرق می‌رود. البته این حرکت ظاهری خورشید بازتاب حرکت مداری زمین است به گرد خورشید. در گذشته می‌پنداشتند که این خورشید است که گرد زمین می‌گردد و خَیاّم هم همین تصور را داشته‌است. هنوز هم در گاهشماری، حرکت ظاهری خورشید را دنبال می‌کنند چون حرکت مداری زمین را نمی‌توان دید. خورشید این حرکت ظاهری را ۳۶۵ و کمی کمتر از ۶ ساعت انجام می‌دهد. توجه کنیم که طول سال ثابت نیست و کم و زیاد می‌شود. ویژگی بسیار مهم گاهشماری خورشیدی و کار خَیاّم این است که ماه‌ها با فصل‌های سال مطابقت دارند. شایان ذکر است که همه گاهشمارها خورشیدی نیستند. برخی به جای حرکت خورشید، ماه را دنبال می‌کنند. اینگونه گاهشمار را قَمَری می‌نامند. مبنای آن فاصله پیاپی دو هلال ماه است که تقریباً ۲۹ روز و نیم می‌شود. سال قمری ۳۵۴ روز است. یعنی ۱۱ روز از سال خورشیدی کوتاه‌تر. در این گاهشمار ماه‌ها ویلان [ویلون] و سرگردانند. مثلا رمضان می‌تواند هم در زمستان بیفتد هم در تابستان...
در گاهشمار ایرانی خَیاّم اما، سال وقتی آغاز می‌شود که خورشید به نقطه دقیقی در آسمان می‌رسد. این نقطه محل برخورد صفحه مسیر حرکت ظاهری سالانه خورشید با استوای زمین است. (نقطه هموگان یا اعتدال بهاری). وقتی خورشید به آنجا می‌رسد یعنی لحظه تحویل سال، شب و روز یکسان می‌شود. بماند که این نقطه هموگان (اعتدال بهاری) ثابت نیست و سالانه کمی بسوی خورشید حرکت می‌کند که بحثی دیگر می‌طلبد. گاهشمار مسیحی (گریگوری) هم خورشیدی است اما شروعش نه آغاز بهار، بلکه نقطه قراردادی نیمه شب در ۳۱ دسامبر است...
تقویم میلادی هر ۳۳۲۰ سال یک روز خطا دارد، اما گاه‌شماری که خَیاّم مبتکر آن بود، هر ۱۰ هزار سال یک بار، دچار یک ثانیه خطا می‌شود. انجام این محاسبات دقیق در آن زمان، بدون استفاده از کامپیوتر و ابزارهای پیشرفته، واقعا یک شاهکار است.
گاهشمار کنونی ایران بر پایه گاهشمار جلالی است که در سال ۱۳۰۴ خورشیدی به همت امثال سیدحسن تقی‌زاده، محمدعلی فروغی و جلال همایی، مجلس شورای ملی به تصویب رساند. در دوران رضاشاه. 
در این گاهشمار، شش ماه اول ۳۱ روز دارند، پنج ماه دیگر هر یک ۳۰ روز و واپسین ماه ۲۹ و گاه ۳۰ روز. اینگونه تقسیم سال، به ماه‌‌هایی با طول‌های گوناگون سازگاری کامل دارد، با این واقعیت که فصل‌های اختر شناختی درازای یکسانی ندارند. بهار و تابستان از پاییز و زمستان درازتر هستند.
  • اضافه کنم که نام دوازده ماه تقویم خورشیدی در ایران، نام‌های باستانی ساسانی امشاسپندان و دیگر ایزدان کیش زرتشتی است. اَمِشاسْپَندان یا اَمِشَه سْپَنتَه جمع امشاسپند است. امشاسپندان از صفات اهورامزدا هستند. چنین به نظر می‌رسد که این‌ها تجریدهایی تشخص‌یافته باشند. اما آن‌ها چیزی بیش از مفاهیمی مجرد بوده‌اند، چرا که زرتشت آنان را محترم می‌شمرده‌است.
  • محاسبات گاه‌شماری خَیاّم، هنوز معتبر است و دقتی به مراتب بالاتر از گاهشماری میلادی دارد. او بدین منظور مدار گردش کرهٔ زمین به دور خورشید را تا ۱۶ رقم اعشار محاسبه نمود. دو نکته:
  1. گاه‌شماری هجری خورشیدی را نخستین بار میرزا عبدالغفارخان نجم‌الدوله اصفهانی (معلم ریاضیات مدرسه دارالفنون) با توجه به گاه‌شماری جلالی استخراج کرد.
  2. ابتکار تغییر گاهشمار رسمی کشور از هجری قمری به هجری شمسی را نخستین بار میرزا عبدالحسین وحیدالملک شیبانی، نماینده دور دوم مجلس شورای ملی پیشنهاد کرد.
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ  
برگردیم به خَیاّم. آن حکیم فرزانه چکیده سده‌ها اندیشه و راه‌جویی و تکاپوی ایران است. نه فقط او، خوارزمی، ابوعبدالله محمد بن عیسی ماهانی، ابوبکر محمد بن حسن[حسین] حاسب کَرجی)، ابوریحان بیرونی، فاضل قوشچی، ابوجعفر خازن، اَبوالْجود (محمد بن احمد بن لیث، خواجه نصیر‌الدین طوسی، ابوالعباس فضل بن حاتم نیریزی، غیاث الدین جمشید کاشانی، ابوسهل کوهی طبرستانی، موسی فرزند شاکر، شرف‌الدین طوسی (مخترع روش محاسبات عددی برای حل معادله درجه سوم) و ابوالوفا بوزجانی...
بسیاری از ما با تاریخ علم و با فرهنگ و تاریخ خودمان بیگانه‌‌ایم. بیشتر ما نمی‌دانیم مفهوم «آلگوریتم» و مثلثات، جبر و تا حدی نظریه اعداد، در ایران زاده شده و اصطلاح «سینوس» و «تانژانت»، ترجمه کلمات «جِیب» و «ظِل» است که ریاضی‌دانان ایرانی ابداع کردند. بی‌خبریم که خَیاّم مبتکر هندسه تحلیلی است و تمام روابط مثلثاتی، از آغاز تا پایان، از مثلثات‏ روی صفحه تا مثلثات کروی، در ایران کشف شده و خواجه‏ نصیر‌الدین طوسی مجموعه‏‌ی آن‏ها را جمع‏‌آوری کرده‌است. نمی‌دانیم غیاث‌الدین جمشید کاشانی عدد پی را تا ۱۹ رقم محاسبه نمود و معادله درجه سوم را که خَیاّم از طریق هندسه گشود، به طریق جبری حل کرده‌ بود. وی برای محاسبه سینوس زاویه یک درجه، توانست ریشه معادله‌های درجة سوم را با بهره‌گیری از روش تکرار با هر دقت دلخواه بیابد.
 
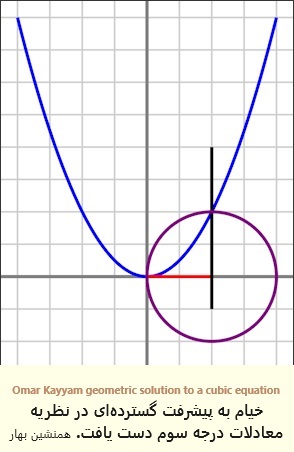
در سالهای دور که در میهن عزیزم بودم، در دانشگاه تهران تصویری از صفحه نخست یکی از رساله‌های خَیاّم را دیدم که به موضوع حل معادلات درجه سه پرداخته بود. وی با روشی مبتنی بر تقاطع دایره و سهمی، انواعی خاص از معادلات درجه سه را حل کرده، نشان می‌داد امکان حل هندسی آن با خط‌کش و پرگار وجود ندارد. در مقاله مربوط به این بحث، صفحه مورد نظر را گذاشته‌ام.
ریاضی‌دانان ایرانی در پیدایش جبر و مقابله و حل معادله‌های درجه اول و دوم و... پیشقدم بودند و در علم حساب هم گامهای بلندی برداشتند. اینکه فقط با ۱۰ علامت، از صفر تا ۹، می‌توانیم هر عددی را بنویسیم، به وسیله آنان در دنیا پخش شد. مورخین تاریخ علم می‌دانند که پایه‌های مثلثات در ایران ریخته شده‌ و ریاضیدانان ایرانی از سده سوم تا نهم هجری تمام زوایای کار مربوط به مثلثات را بررسی و روابط آنها را کشف کردند و اما خَیاّم. او نزد ابوالحسن انباری، حکیم و هندسه‌دان هم روزگارش، کتاب مَجِسطی بطلمیوس، یکی از مهمترین کتابهای نجوم را خواند. وی شاگرد ریاضی‌دان زرتشتی، بهمنیار هم بود. کارهای خیام در ریاضی ازجمله اصل توازی در جبر، و طبقه‌بندی و حل معادلات درجه سوم، شایان بسی تامل است. نقطه نظرات خَیاّم در این مورد، او را نسبت به عصر خویش، چهار قرن به دوران معاصر نزدیک‌تر نشان می‌دهد. یعنی بیشتر به عصر پاسکال و دکارت و نیوتن، تا زمانه خود خَیاّم. 
ـــــــــــــــــــــــــــــــــــــــــــ.
معادله یک گزاره ریاضیِ تشکیل شده از یک نمادِ مساوی بین دو عبارت جبری است که دارای مقدار یکسان هستند. به زبان ساده‌تر، معادله یک تساوی بین دو عبارت جبری است. تا آنجا که من می‌دانم خَیاّم اولین کسی است که به تحقیق منظم علمی در معادلات درجات اول و دوم و سوم پرداخته، آنها را طبقه‌بندی کرده و حل هندسی انواع معادلات درجه سوم از روی تقاطع منحنی‌های مخروطی را مورد تحقیق قرار داده‌است. کتاب جبر و مقابله او (رساله فی البراهین علی مسائل الجبر و المقابله) شاهد این مدعا است. قبل از خَیاّم معادلات درجه اول و درجه دوم حل شده بود و چون حل معادله درجه سوم مورد نیاز بود، خَیاّم به حل هندسی آن اقدام کرد. البته جلو تر «ابوعبدالله محمد بن عیسی ماهانی» نویسنده رساله «تفسیر المقاله العاشره من کتاب اقلیدس» به دنبال حل معادله درجه سوم بود. خَیاّم در این باره می‌گوید «ریاضیون قدیم غیر عربی‌زبان به چیزی از مقوله جبر و مقابله پی نبردند و از اطلاعات ایشان در این باب چیزی به ما نرسیده ولی متاخرین آشنا به زبان ما اول کسی که به نوع ثلاثی از این ۱۴ قسم برخورده‌، ماهانی مهندس است.»
خَیاّم تمام معادلات تا درجه سوم را بر حسب ضرایب به ۱۴ صنف دسته‌بندی و حل کرد و در حمله فوق به آن اشاره کرده‌است. در اوایل قرن نهم غیاث‌الدین جمشید کاشانی (الکاشی)، روش دوگانه‌ای را برای یافتن ارزش عددی ریشه‌های معادلات درجه سه با دقت زیادی ابداع کرد. در نیمه قرن شانزدهم «جرلامو کاردانو» Gerolamo Cardano هم فرمولی برای حل معادلات درجه سه عرضه کرد. 
ـــــــــــــــــــــــــــــــــــــــــــ.
رساله فی البراهین علی مسائل الجبر و المقابله نخستین‌بار در شهر لایدن هلند پیدا شد و مورد توجه ریاضیدانان ازجمله Franz Wöpcke فرانتس وُپکه قرار گرفت. وُپکه متن آنرا با ترجمه فرانسوی و حواشی و ملحقات سال ۱۸۵۱ منتشر نمود. سال ۱۹۳۱ به انگلیسی و سال ۱۹۵۳ به روسی هم ترجمه شد. متن عربی و ترجمه مختصری از آن با حواشی و ضمائمی تحت عنوان جبر و مقابله خَیاّم در ۱۳۱۷ خورشیدی منتشر شد. این کار، نخستین معرفی خَیاّم به عنوان ریاضی‌دان در یک اثر مستقل به فارسی بود. دکتر غلامحسین مصاحب در سال ۱۳۳۹ متن کامل رساله فی البراهین علی مسائل الجبر و المقابله را نیز به فارسی منتشر نمود و با کتاب «حکیم عمر خَیاّم به عنوان عالم جبر» گام مهمی در معرفی خَیاّم ریاضی‌دان برداشت. خَیاّم در یکی از آثارش نوشته: «ما را رساله‌ای است که در آن نشان داده‌ایم چگونه پایه مربع مربع، مربع مکعب، مکعب مکعب و غیر آنرا، هر قدر باشد، می‌توان مُعیّن کرد که قبلاً سابقه نداشت.» 
 
خَیاّم در کتاب مسایل حساب، به یافتن ریشه‌ی nام معادلات پرداخت و مسئله ریاضی موسوم به «قضیه دو جمله‌ای» (binomial theorem) را سده‌ها سال پیش از نیوتن، حل کرد. او در تحقیقی که برای حل معادلات جبری انجام داده‌است به بسط قوای مختلف یک «دو جمله‌ای» نیاز ‌داشته و تشکیل ضرائب این بسط و گسترش را بصورت قاعده و دستوری که امروزه به «مثلث پاسکال» معروف است کشف کرده بود. بسط دوجمله‌ای جبری امروزه معمولاً بنام بسط دوجمله‌ای نیوتن معروف است چرا که گفته می‌شد وی نخستین بار این محاسبات را مُدوّن کرده‌است. واقعش خَیاّم در کارهای خود این بسط و قانون تشکیل مراتب آنرا بکار برده‌ بود. بعبارت دیگر دوجمله‌ای نیوتن و مثلث پاسکال حدود ۴ قرن پیش از آنها توسط خَیاّم کشف و وضع شده‌اند. بعد از ابوسهل کوهی طبرستانی، عمر خَیاّم، در سال ۱۰۷۸ میلادی (۴۵۶ خورشیدی)، سری دوجمله‌ای Binomial series را برای کل اعداد مثبت کشف کرد، این فرمول همان بسط دو جمله‌ایِ (a+b) به توان n است. خَیاّم تا توان ۱۲ را محاسبه کرده بود و حدود ۵۰۰ سال بعد (۱۶۶۹ میلادی)، نیوتن آن را گسترش داد. 
برای تنظیم ضریبهای بسط دوجمله‌ای، مثلثی در نظر گرفته شد.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
در این مثلث از سطر سوم به بعد، هر عدد برابر با مجموع اعداد بالا و سمت چپ آن در سطر قبل است و بنابراین می‌توان آنرا تا هر جا که لازم باشد ادامه داد. هر سطر این مثلث ضریب‌های بسط دوجمله‌ای را در یکی از حالت‌ها بدست می‌دهد بطوری که n همان شماره سطر باشد.
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
برگردیم به معادلات درجه سوم
در این زمینه خَیاّم، به پیشرفت گسترده‌ای دست یافت. وی ابتدا شرح داد که یک معادله درجه سوم می‌تواند بیش از یک ریشه داشته‌باشد. وی همچنین به یک جواب هندسی برای دسته‌ای از این معادلات دست یافت. در کتابی که بعدها نوشت معادلات درجه سوم را در حالت کلی طبقه‌بندی کرد و توانست جوابی عمومی با استفاده از مقاطع مخروطی ارائه کند. در مورد معادلات درجه سوم خَیاّم اول کسی است که آنها را طبقه‌بندی کرده، او در کتاب «فی البراهین علی المسائل الجبر و المقابله»، همچنین در رساله‌ تحلیل یک مسئله هندسی، به معادلهٔ درجه سوم و حل آن به وسیله قطوع مخروطی اشاره می‌کند. 
از آقای دکتر ناصر کنعانی فیزیکدان ایرانی و استاد دانشگاه فنی برلین شنیدم بدون اشراف به معادلات درجه سوم (خَیاّم) معماران مسجد جامع اصفهان نمی‌توانستند کار خود را پیش ببرند. خَیاّم اولین کسی است که هندسه تحلیلی را برای حل معادلات جبری بکار برده‌است. (چهار قرن قبل از دکارت)
 
اگر توجه شود که در زمان خَیاّم عددنویسی بصورت امروز و تشکیل معادلات جبری با علائم و نشانه‌های کنونی وجود نداشته‌است، اهمیت و ارزش کارهای ریاضی آن دانشور ارجمند بهتر درک خواهد شد. جورج سارتن با نام بردن از خَیاّم به عنوان یکی از بزرگ‌ترین ریاضی‌دانان قرون وسطی می‌نویسد: خَیاّم اول کسی است که به تحقیق منظم علمی در معادلات درجات اول و دوم و سوم پرداخته‌است. رسالهٔ وی در علم جبر، که این تحقیقات را در بردارد، معرف یک فکر منظم علمی است...
خَیاّم، در مقدمهٔ رسالهٔ (جبر و مقابله) که بزبان عربی نوشته، از روزگار شکایت می‌کند. که مضمون آن چنین است: «شاهد بودیم که دانشوران رفتند و بگروهی که تعدادشان اندک و رنج‌شان بسیار بود، محدود شدند که زندگی سخت خود را صرف تحقیقات و اکتشافات علمی کردند؛ بیشترشان حق را با باطل می‌پوشانند، تزویر و ظاهرسازی پیشه کرده و آن مقدار معرفتی را هم که دارند، برای اغراض پست مادی بکار می‌برند...»
برای من درد دل خَیاّم، سخنی را تداعی می‌کند که کهن‌سالان لرستانی گفته اند: «هر کجا ری می‌کنم سیا زمین‌ه» به هر جا روی می‌آورم جز سیاهی نمی‌بینم.
 [Har koja ri mikonam siazamine]
...
حالا به ملاحظات خَیاّم در مورد اصول اقلیدس بپردازیم. 
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
کتاب اصول هندسهٔ اقلیدس (Στοιχεῖα Stoicheia) حدود ۳۰۰ سال قبل از میلاد توسط وی تألیف شده و پنج اصلِ موضوعهٔ را در برداشت که از شرح آن می‌گذرم.
اقلیدس گزاره زیر را قطعی و مُسلّم پذیرفته بود: از نقطه‌ای مفروض در خارج یک خط می‌توان یک خط و تنها یک خط به موازات آن رسم کرد. در این مورد (اصل خطوط متوازی)، خَیاّم رساله‌ای نوشت که عنوانش این بود: «فی شرحُ ما اَشْکَلَ من مصادرات اقلیدس» شرح در مورد بعضی مسائل که در تحریرات اقلیدس مشکل به نظر می‌رسد. رساله مزبور شامل سه فصل است:
۱- در باره قضیه معروف اقلیدس در باب خطوط موازی
۲- در باب نسبت‌ها و تناسب‌ها
۳- در باب نسبت‌های ترکیبی
بعدا معلوم شد تلاش‌های خَیاّم و ریاضیدانان پیش و بعد از او از مقوله بُن‌بست‌های ریاضی بود که در رشد و توسعه نهایی هندسه اهمیت داشت.
...
دکتر تقی ارانی رساله فی شرحُ ما اَشْکَلَ من مصادرات اقلیدس را در سال ۱۳۱۴ با مقدمه‌ای مفصل منتشر نمود و بعدها استاد جلال همایی (که خَیاّمی نامه را هم نوشته) به فارسی ترجمه کرد.
در رساله مزبور، خَیاّم تعریف اقلیدس از نسبت‌های برابر را بازتعریف نموده،اعدادی را مطرح می‌کند که می‌توانند اعشار نامتناهی داشته باشند و یک نسبت را تعریف کنند. گفته می‌شود خَیاّم با این کار انقلابی در اصول اعداد را آغاز کرد. 
تحلیل خَیاّم در این رساله کم و بیش به کار دانشمندان ریاضی اوائل قرن نوزدهم شباهت دارد خودش گفته‌است: «شاید ترتیبی که من برای توضیح و توجیه این حکم بکار می‌برم روشن‌تر و منطقی‌تر از طریقه اقلیدس باشد». 
خَیاّم در کتاب «فی شرحُ ما اَشْکَلَ من مصادرات اقلیدس»، نسبت به اصول هندسهٔ اقلیدسی که صدها سال کتاب درسی سراسر دنیا بود، تردید کرد و بی‌آنکه بداند بیانی برای هندسه نااقلیدسی ارائه نمود. بدیهی است که ایجاد چنین هندسه‌ای برای آن دوره بسیار زود بود، بیش از ۷۰۰ سال بعد، همان روش خَیاّم مبنای کار 
ریاضی‌دان روس، نیکلای ایوانوویچ لوباچفسکی (۱۷۹۲ – ۱۸۵۶)، و ریاضی‌دان آلمانی برنهارد ریمان ‏(۱۸۲۶–۱۸۶۶) در ساختن هندسهٔ غیر اقلیدسی قرار گرفت. تلاش‌های ریاضی‌دان ایتالیایی «جیرلامو ساکری» (۱۶۶۷–۱۷۳۷) هم، بعدها در ابداع هندسه‌های نااقلیدسی پی گرفته شد. یکی از ابزارهایی که جیرلامو ساکری در کار خود ایجاد کرد که اکنون چهارضلعی ساکری Saccheri quadrilateral نامیده می‌شود، سابقه‌ای در رساله خَیاّم (فی شرحُ ما اَشْکَلَ من مصادرات اقلیدس) دارد. البته خَیاّم از چهارضلعی استفاده چندانی نکرد، در حالی که جیرلامو ساکری عمیقاً به آن پرداخت.
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
نوپیدا کردن نظریه‌ای دربارهٔ نسبت‌های هم‌ارز با نظریهٔ اقلیدس نیز از مهم‌ترین کارهای خَیاّم است. بین منطق و ریاضیات در نظر خَیاّم نوعی بستگی محکم وجود دارد که اصل توازی را بصورتی دیگر عنوان می‌کند که به نطر او منطقی‌تر از سبک اقلیدس است. از نگاه و دیدگاه خَیاّم، هندسه علم به اشکال مجرد است که در فضای مجرد مستغرق‌اند و این نکته بسیار مهم است زیرا نزد یونانیان، فضا، معتبر نبود و مکان اجسام بنا بر رأی ارسطو جایگاه اشکال و اجرام محسوب می‌گردید و ما اکنون می‌دانیم که تصور فضای مجرد در پیشرفت علوم ریاضی و فیزیکی چه کمک شایانی نموده‌است. پیوستگی منطق و ریاضیات در نظر خَیاّم باصلی منجر می‌شود که اکنون در فلسغه علمی یکی از مبانی بنیانگذاری علوم محسوب می‌گردد و آن اصل علیت بمفهوم علمی است. بستگی علّی بین آثار مشهود هرچه باشد، کیفیت بروز این آثار ثابت است و خَیاّم به این مطلب توجه دقیقی دارد و در رباعیات خودش هم به آن اشاره کرده‌: «تا بوده نشان بودنی‌ها بوده‌است».
...
خَیاّم در رساله خود درباره اعداد گنگ (اصم) هم نظراتی را بیان می‌کند. در ریاضیات، اعداد گنگ Irrational Numbers، تمام اعداد حقیقی را شامل می‌شوند که گویا نباشند و نمی‌شود آنها را به صورت نسبت دو عدد صحیح نوشت. در ریاضیات کلاسیک «رادیکال دو»، رایج‌ترین گزینه برای اثبات وجود اعداد گنگ است. در واقع ثابت می‌شود که عدد گویایی موجود نیست که مربع آن برابر با ۲ شود.  
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
از خَیاّم چندین و چند رساله یافت شده‌ که شماری به فارسی است ازجمله رباعیات، «در علم کلیات»، نوروزنامه (که البته منسوب به اوست) و برگردان خطبه ابن سینا. بقیه را به عربی نوشته‌است. به شماری از آنها اشاره می‌کنم:
  • فی الوجود
  • فی الکُون و التکلیف
  • ضروره التضاد فی العالم و الجبر و البقا
  • الضیاء العقلی فی موضوع العلم الکلی
  • الجواب عن ثلاث مسائل (جوابٍ لثلاث المسائل)
  • فی قسمة ربع الدائرة (در هندسه)
  • القول علی اجناس الذی بالاربعة (در مورد موسیقی) 
  • رسالة فی الاحتیالِ لِمعرفة مقدارَیِ الذهَبِ و الفضّةِ فی جسمٍ مرکّبٍ منهما

خَیاّم در رساله مزبوربه تعیین عیار طلا و نقره و شِمشی که از این دو فلز ترکیب شده‌، اشاره می‌کند که درواقع توضیح روش ارشمیدس و تجربه مشهور اوست. خَیاّم او در رساله «فی قسم ربع ‌الدائره» برای تقسیم ربع دایره، روشی ابداع کرد تا از طریق آن روابط خاص بین پاره خط‌ها را محاسبه کند. او این مسئله را به یک معادله درجه سوم کاهش داد که با استفاده از مقاطع مخروطی حل می‌شود. نسخه خطی رساله مزبور در کتابخانه مرکزی دانشگاه تهران موجود است و سال ۱۳۳۹ با ترجمه فارسی منتشر شد. به انگلیسی و فرانسوی و روسی هم ترجمه شده‌است.
...
ابوالحسن علی بن زید بیهقی، خَیاّم را از خانواده‌ای ریشه‌دار می‌دانست که از دیرباز در نیشابور می‌زیسته‌اند. به گفتة بیهقی، عین القضات همدانی و علی بن محمد حجازی قاینی از شاگردان خَیاّم بوده‌اند. ابوالقاسم زمخشری هم محضر خَیاّم را درک کرده بود. بیهقی به حضور امام محمد غزالی در مجلس خَیاّم اشاره کرده و اینکه وی در خراسان با خَیاّم دیدار داشته‌است.گویا غزالی اشارات [لإشارات و التنبیهات‌] ابوعلی سینا را نزد خَیاّم خوانده‌است.
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
به نظر من نگاه و دیدگاه‌ خَیاّم و غزالی تفاوت اساسی داشت. نوروزنامه کتابی منسوب به خَیاّم در دسترس است، او در این کتاب که به کوشش مجتبی مینوی (تهران ۱۳۱۲ش) و نیز علی حصوری (تهران ۱۳۴۳ش) منتشر شده‌است، به نوروز و جشنهای ایرانی ارج می‌نهد اما از نظر غزالی «نوروز و سده باید مندرس شود و کسی نام آن را نبرد و اظهار شعار گبران حرام است.» غزالی در تضاد عقل و شرع، مثل سایر متکلمان، عقل را عملاً سینه دیوار می‌گذارد. وی بعد از نگارش کتاب «مقاصد الفلاسفه»، به بهانه رو کردن تناقضات فیلسوفان، فلسفه را زغنبوت و زهر هلاهل جلوه ‌داد و در کتاب «تهافت الفلاسفه»(تناقض‌گویی فیلسوفان) که یکی از پر اثر‌ ترین(و نه مفید ترین)، کتاب‌هایی بوده که در تاریخ بشر نوشته شده، با انگیزه‌های اعتقادی(فقیهانه و نه فیلسوفانه)، امثال فارابی و ابن سینا را به محاکمه کشید و حکم کفر صادر ‌کرد. سایه سنگین‌ غزالی قرن‌ها اجازه نداد گرایش به فلسفه احیا شود. فلسفه از نظر غزالی اصلاً علم به حساب نمی‌آمد.
در مقدمه چهارم کتاب تهافت الفلاسفه، گرایش فیلسوفان به ریاضیات و منطق را هم زیر سئوال می‌برَد. او با چوب تکفیری که در دست داشت، عملاً مصونیت اظهار نظر را از دیگران گرفته بود و البته تصور نمی‌کرد دود این آتش - آتش تنگ نظری و تعصب - به چشم خودش هم خواهد رفت. من در مقاله و ویدئوی نوروز و ابوحامد محمد غزالی به شرح‌تر توضیح داده‌ام. 
...
آنچه برای من اهمیت دارد این است که خیام در چنبره حیرت و اندوه، توجه می‌دهد که گذشته و آینده، همین اکنون است.
از دی که گذشت هیچ از او یاد مکن
فردا که نیامده‌ست فریاد مکن

 

بگذریم که انسان موجودی خاطره‌گراست و کوله‌بار گذشته بر دوشش سنگینی می‌کند. او همچنین نمی‌تواند در آرزوی صبح سپید نباشد. به نظر خیام اما گذشته و آینده، همین اکنون است. پس باید به شور و شادی اصالت داد و به بهار اقتدا کرد. چرا که در راه رهزنانند. 
ذخیره‌ای بنه از رنگ و بوی فصل بهار 
که می‌رسند ز پی رهزنان بهمن و دی
منابع این بحث
  • رباعیات خَیاّم. با تصحیح، مقدمه و حواشی محمدعلی فروغی و قاسم غنی.
  • علی بن یوسف قفطی، تاریخ الحکما
  • ابوالقاسم قربانی، زندگی‌نامهٔ ریاضیدانان دورهٔ اسلامی از سدهٔ سوم تا سدهٔ یازدهم هجری
  • عبداللّه بن محمد نجم رازی، مرصادالعباد
  • جلال الدین همائی، خَیاّمی نامه
  • جلال خالقی مطلق، خَیاّم و موضوع شاعری او
  • رحیم رضازاده ملک‌، دانشنامه خَیاّمی (مجموعه رسائل علمی، فلسفی و ادبی خیاّم)
  • روزنفلد، ب. آ؛ و یوشکویچ، آ.ب، «نظریهٔ خَیاّم دربارهٔ خطوط موازی»، ترجمهٔ پرویز شهریاری
  • محمد محیط طباطبائی، خَیاّمی یا خَیاّم
  • صادق هدایت، ترانه‌های خَیاّم
  • جهانگیر هدایت، مجموعه آثار صادق هدایت دربارة خَیاّم
  • علی دشتی، دَمی با خَیاّم
  • غلام‌حسین صدری افشار،، «آثار مربوط به تاریخ ریاضیات در زبان فارسی»
  • محمدمهدی فولادوند، خَیاّم‌شناسی
  • غلامحسن مصاحب، حکیم عُمَر خَیاّم به عنوان عالم جبر
  • غلامحسن مصاحب، جبر و مقابلهٔ خَیاّم
  • مجتبی مینوی، عمر خَیاّم، نوروزنامه
  • داریوش آشوری، راه حل ایرانی خیام در مواجه با جهان گذرا (کفتگو با صادق صبا)
  • عبدالکریم سروش، خیام در حافظه حافظ
  • احمد بیرشک، تقویم جلالی خیام
  • محمد استعلامی، دیدگاه خیام به زندگی
  • نصرت الله نوح، خیام و رباعیاتش
  • حسن نظریان، نوزده مقاله دربارهٔ حکیم عُمَر خَیاّم نیشابوری
  • جلال مصطفوی، استفادهٔ دانشمندان مغرب زمین از جبر و مقابلهٔ خَیاّم
  • محمد باقری، بین میخانه و مدرسه: عمر خَیاّم دانشمند
  • حسین معصومی همدانی، نگاهی به زندگی خَیاّم نیشابوری
  • سعید حسام‌پور و کاووس حسنلی، رویکردهای پنج‌گانه در خَیاّم‌شناسی 
  • علیرضا ذکاوتی قراگزلو، عمر خَیاّم نیشابوری
  • علی اصغر سیدغراب و...، فیلسوف تودار و رباعیات بودار
  • فیروزه عبدالله‌اوه، ناتالیا چالیسوا و چارلز ملویل، پذیرش خَیاّم در روسیه: از متن تا تصویر)
  • اشکان گرشاسبی، واکاوی مفاهیم علمی و اعداد در رباعیات خیام، و...
  • دبورا کنت ، دیوید موراکی، حل هندسی معادلات درجه سوم توسط عمر خیام...
  • حسن صادقی سمرجانی، علی یحیایی، خیام در مقام اعتراض به سیاست های خردستیز عصر سلجوقی
  • جعفر آقایان چاووشی، سیری در افکار علمی و فلسفی حکیم عمر خَیاّم نیشابوری
  • داریوش شایگان، «خَیاّم: شاعر لحظه‌های برق آسای حضور»، ترجمه نازی عظیما
  • سیدحسین نصر، علم و تمدن در اسلام، ترجمهٔ احمد آرام
  • اسماعیل یکانی، عمر خیام نادرهٔ ایام
  • جورج سارتون، مقدمه بر تاریخ علم، جلد اول: از هومر تا عمر خَیاّم، ترجمه غلامحسین صدری افشار
  • ناصر کنعانی، عمر خیام ستاره شناس و ریاضیدان
  • یوهانس پیتر دوبروین Johannes Pieter de Bruijn، «دیگر رباعیات فارسی در هلند - گلزار دانش حسین آزاد»
  • همنشین بهار، خَیاّم که خیمه‌های حکمت می‌دوخت
 
 
    • Tikkanen Amy. "Omar Khayyam: Persian poet and astronomer". Encyclopaedia Britannica.
    • O Connor, John J.; Robertson, Edmund F. "Omar Khayyam",
    • M. Vali Siadat &Alana Tholen, Omar Khayyam: Geometric Algebra and Cubic Equations
    • Struik, D.J. "Omar Khayyam, mathematician"
    • Browne, E.G. "Yet More Light on “Umar-i-Khayyam". Journal of the Royal Asiatic Society of Great Britain and Ireland.
    • Rosenfeld, Boris A. "Umar al-Khayyam". Encyclopaedia of the History of Science,
    • "Khayyam, As Mathematician". Encyclopædia Iranica.
    • Nethington, Amanda "Achieving Philosophical Perfection: Omar Khayyams Successful Replacement of Euclids Parallel Postulate"
    • Smith, D.E. "Euclid, Omar Khayyam, and Saccheri"(جیرولامو ساکری)
    • Eves, H. "Omar Khayyams Solution of Cubic Equations". Mathematics Teacher.
    • Kent, Deborah A. Muraki, David J. "A Geometric Solution of a Cubic by Omar Khayyam …
    • Kennedy, Evelyn "Omar Khayyam". The Mathematics Teacher.
    • Amir-Moez, A.R. "A Paper of Omar Khayyam". Scripta Mathematica.
    • Amir-Moez, A. R. "Khayyams Solution of Cubic Equations". This paper contains an extension by Mohsen Hashtroodi of Khayyams method to degree four equations.
    • Coolidge, J.L. "The Story of the Binomial Theorem". American Mathematical Monthly.
    • Nichols, Susan. Al-Karaji: Tenth-Century Mathematician and Engineer.
    • "How Omar Khayyam changed the way people measure time". The Independent. 17 May 2019
    • Roshdi Rashed, Al-Khayyam mathematicien, en collaboration avec B. Vahabzadeh, Paris, Librairie Blanchard, 1999
    • Khayyam in de Nederlandse Muziek, door prof. Rokus de Groot, Universiteit van Amsterdam
    • Крамар ФЗ. Об исследованиях Омара Хайяма и Насиреддина Туси по теории параллельных линий. — Алма-Ата, 1964
 
░▒▓ همه نوشته‌ها و ویدئوها در آدرس زیر است: 
...
همنشین بهار 

برای ارسال این مطلب به فیس‌بوک، آیکون زیر را کلیک کنید:
facebook